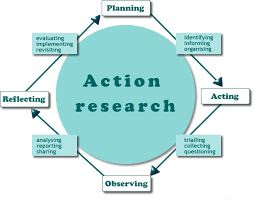
An action research study begins with an observation of a situation that
raises some questions regarding a gap between the intention and the practice (Kumar,2005). In addressing such situations, the teachers need to develop some personal
assumptions which is the real start of the action research process. Observation
in a situation demands an inquiry that leads to a guiding question for research purposes. During the action research which I conducted, followed the
procedures of action research such as identifying a problem, reconnaissance,
planning, taking the first action step, evaluating, amending the plan, and
taking the second action step as suggested by (Lewin cited in Smith, 2001).
Identification of the problem area or
initial idea
The starting point of an action research process is the identification
of the problem area or a general idea. In my action research, I identified the
problem of understanding geometry involving proving theorems in secondary
school classes. In fact, it was my own experience that I hardly understood the
theorems to prove during my school life. Some students I found complained that
theorems in geometry were difficult to prove in secondary classes. A careful investigation
was needed at the first stage of my research to state the problem in simple
language, concise and meaningful (Gay & Airasian, 2003).
Reconnaissance or fact-finding
Before deciding on any action to take, the collection of data is an important
step to find facts about the problem or issues to be studied. According to
Burns (2000), there are many sources to collect data such as observation in a
specific context, interviews, questionnaires, test records, samples of students'
work, and reflective journals.
In my action research, I observed the teaching and learning process for some
days in a mathematics classroom where one of my colleague mathematics teachers
taught proving theorems in geometry. I
completed a checklist in each lesson while observing students’ responses during
the teaching and learning process to investigate the research problem. In the
checklist, I used a scale of 1-5 for each response where 1 was used for less than 5
students, 2 for 6-10 students, 3 for 11-15 students, 4 for 16-25 students and 5
used to show more than 25 students out of 33 students. All three completed
checklists provided the information regarding the problem as follows.
The teacher used the lecture method to teach theorems in three lessons and
provided opportunities for the students to share their ideas with their
colleagues. From the analysis of the checklists completed during three lessons, I found that less than 5 students out of 33 students discussed some points with
each other when the teacher asked them to share their learning in their pairs. The rest of the students were quiet looking at the teacher’s proved theorem on the blackboard. During an informal discussion, I asked a mathematics teacher in the
school about the reason for the lack of sharing ideas among the students. The
reason I found this was that the students do not clearly understand geometrical
concepts in middle classes.
The students did not provide any response which showed their prior
knowledge and command over the concepts involved in the theorems. Analysis of
the checklist revealed that the on the teacher’s instruction to solve the
theorem on the blackboard during the presentation stage of the lesson, less than 5
students proved a part of the theorem individually on the blackboard or in
their notebooks. The comments which I gave in the checklist during observation
in three lessons indicated that not a single response was observed among the
students regarding their prior knowledge and its application in current
learning of proving theorems. The filled checklist showed that fewer than 5 students
showed responses to agree or disagree with the arguments of each other
through examples to clarify their misconceptions.
The gathered evidence indicated that the actual cause of the problem was
the students’ low level of understanding of geometry. After finding the problem
at the grassroots level I planned to address the problem in my action research
process.
Planning
I designed a plan of action after the fact-finding stage that allowed me
to take action steps in the classroom to address the problem. The action plan
included the selection of the procedures, choice of materials, resources,
teaching methods, and allocations of tasks. While planning for my action
research I discussed with the head teacher, another mathematics teacher, and the
staff of the school regarding time, resources, and suggestions during the
process. Burns (2000) emphasizes discussions and negotiations with the
teachers, principals, and supervisors regarding the actions to be taken in the
situation. This helps the teachers who undertake action research to improve
their performance through the influences of participants on planned activities
during the research process.
Taking the first action step
I planned to start my actions to increase the students’ level of content
in geometry because insufficient content among the students at this level
caused poor performance in the classroom situation (Chissick, 2004).
Therefore improvement of students’ level of content in geometry started by
enabling them to recognize and analyze the geometrical figures (Heile, as cited
in Pegg, 2001; Siddiqui, 2005).
Evaluation of the results
The effects of the intervention were assessed to determine the
improvements that occurred in the teaching and learning process. Ferrance
(2000) stated that positive changes are judged on the basis of the
supporting evidence which is provided by the data.
The evaluation was the final stage where the procedure of action research was completed.
In my research study, the evaluation of actions and their effects was carried
out on the basis of data gathered through observation, pre and post-test, and my
reflective journal.

0 Comments
Post a Comment